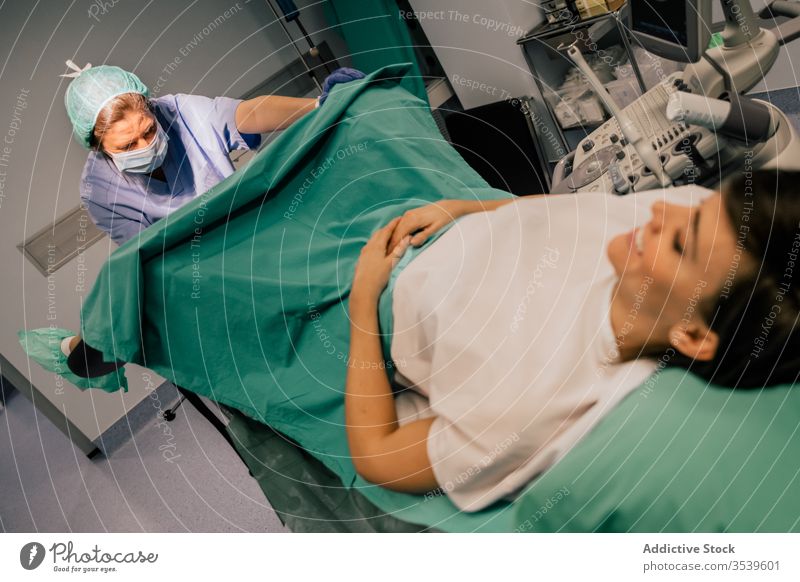
Junge frau liegt im gynäkologischen stuhl während der gynäkologischen fototapete • fototapeten Professionalität, medicals, Analyse | myloview.de
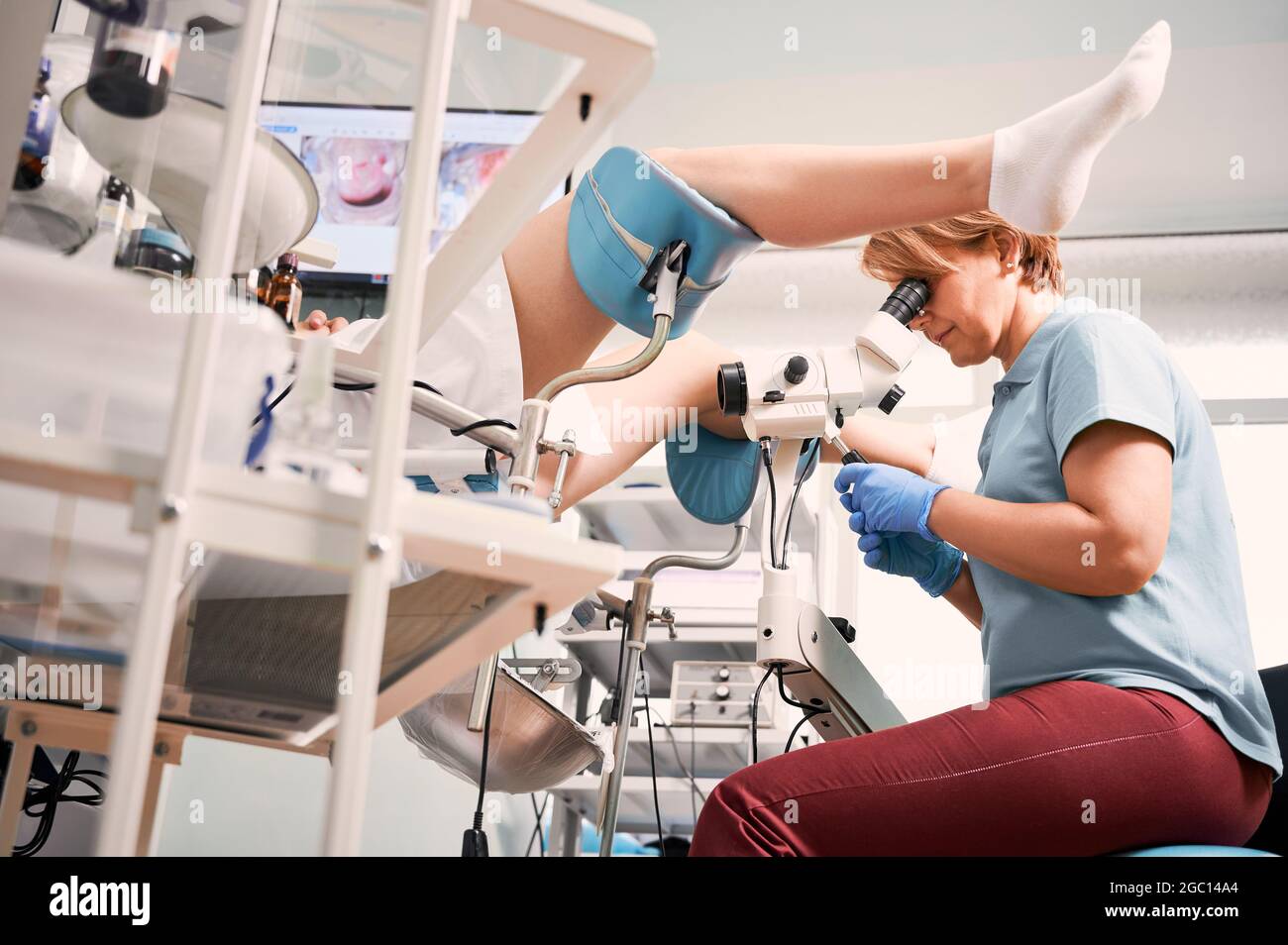
Weibliche Gynäkologin, die Patienten mit Kolposkop in der gynäkologischen Klinik untersucht. Frau, die auf einem Stuhl sitzt, während der Arzt die Kolposkopie untersucht. Konz Stockfotografie - Alamy

Gynäkologe, Der Einen Patienten Sitzt Auf Prüfung Gynäkologischem Stuhl Stockbild - Bild von gynäkologe, büro: 207174957

Schöne Junge Arzt Sitzt Auf Dem Gynäkologischen Stuhl In Ihrem Büro Lizenzfreie Fotos, Bilder Und Stock Fotografie. Image 4695042.
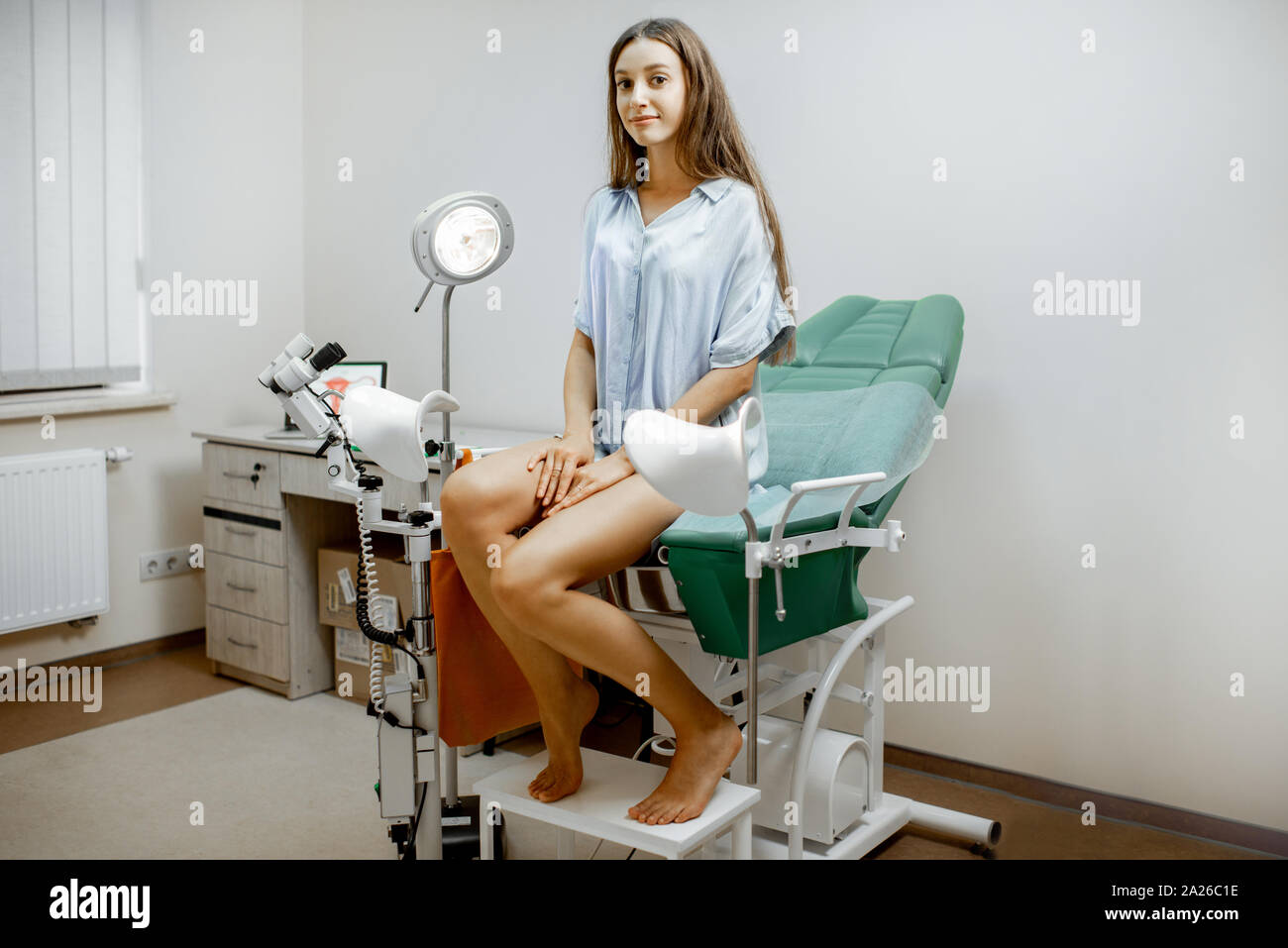
Frau sitzt auf dem gynäkologischen Stuhl, bevor Sie eine ärztliche Untersuchung durch einen Gynäkologen im Büro Stockfotografie - Alamy
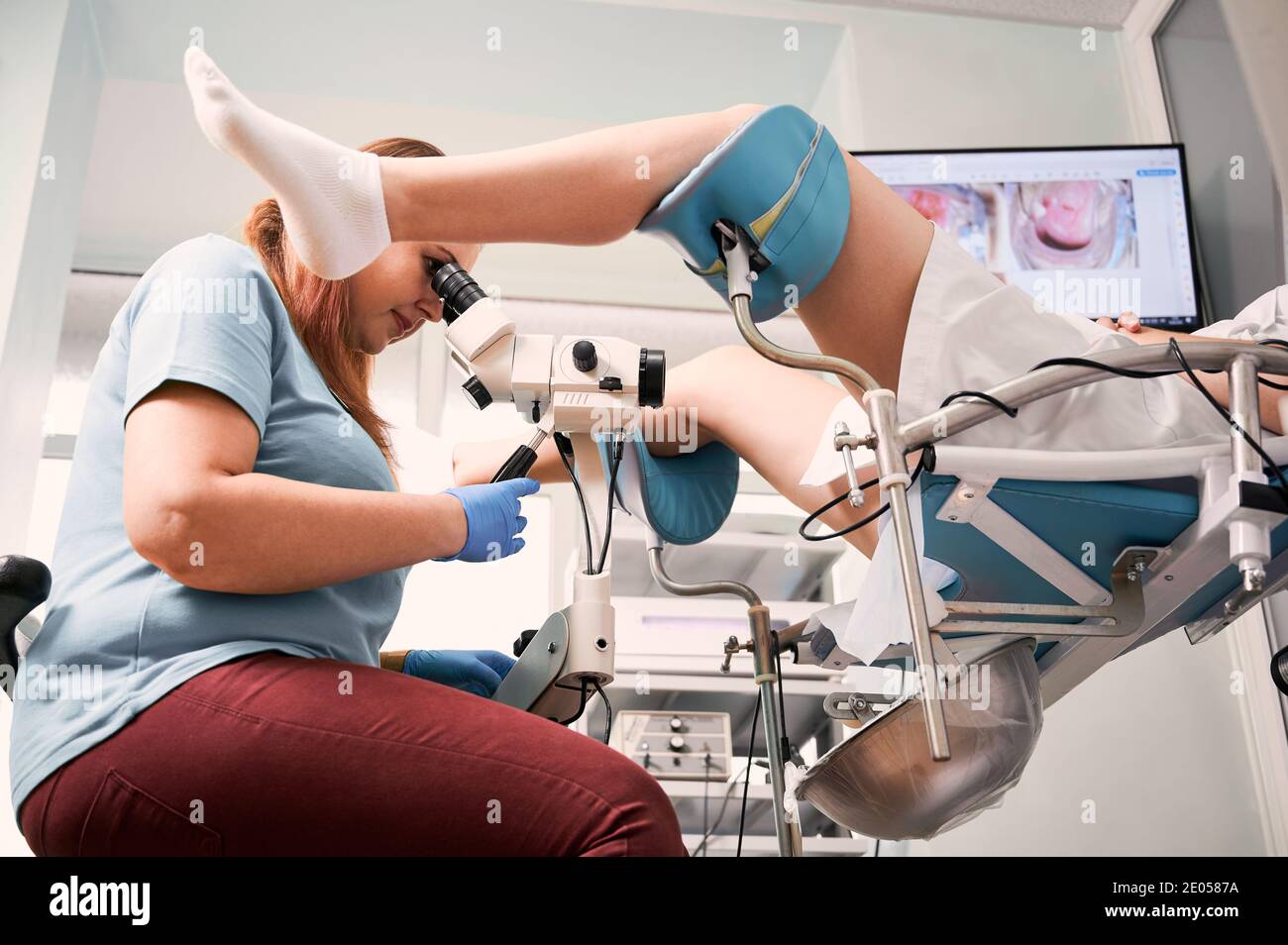
Seitenansicht des Gynäkologen mit Kolposkop während der Untersuchung Frau in der gynäkologischen Klinik. Weibliche Patientin sitzt in gynäkologischen Stuhl, während Arzt tun Kolposkopie Untersuchung. Konzept der Gynäkologie Stockfotografie - Alamy
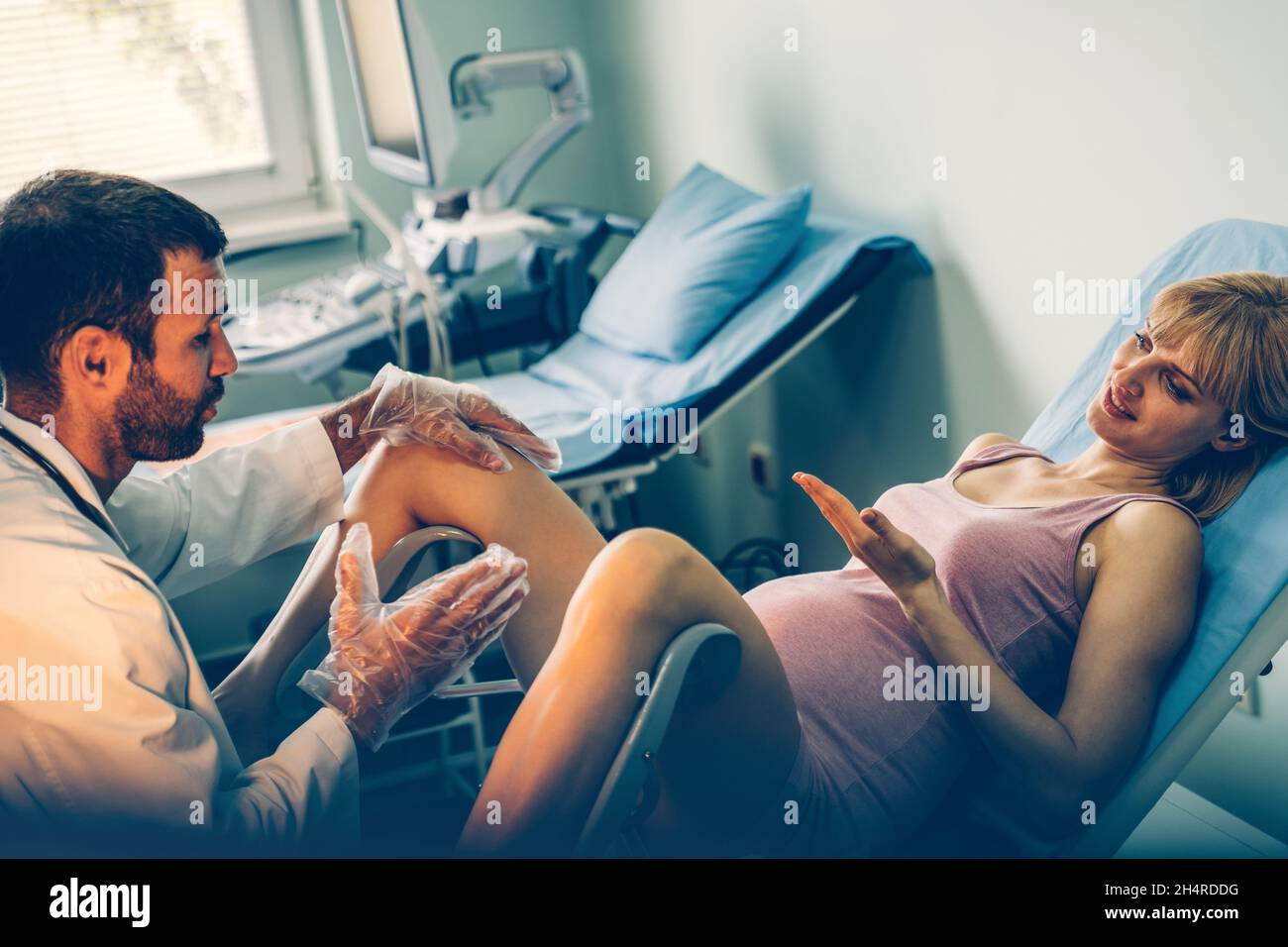
Gynäkologe Untersuchung Frau Patientin in einem gynäkologischen Stuhl. Weibliches Gesundheitskonzept Stockfotografie - Alamy
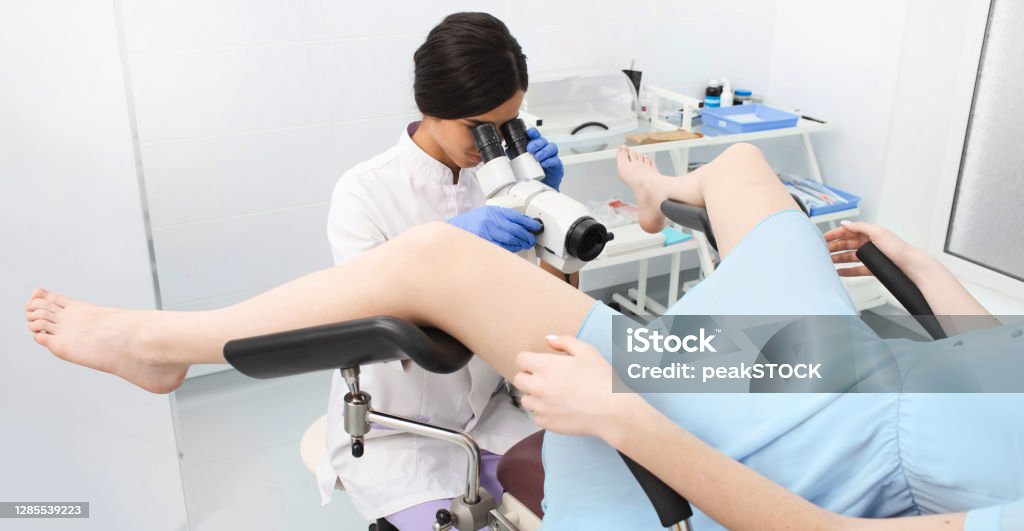
Frauen Mit Einer Gebärmutterhalsuntersuchung Durch Ihren Gynäkologen Der Auf Einem Gynäkologischen Stuhl Liegt Kolposkopie Diagnose Von Gebärmutterhalskrebs Stockfoto und mehr Bilder von Gebärmutterhalskrebs - iStock

Gynäkologe, Der Auf Einem Gynäkologischen Stuhl Sitzt Stockbild - Bild von obacht, ausrüstung: 206889783
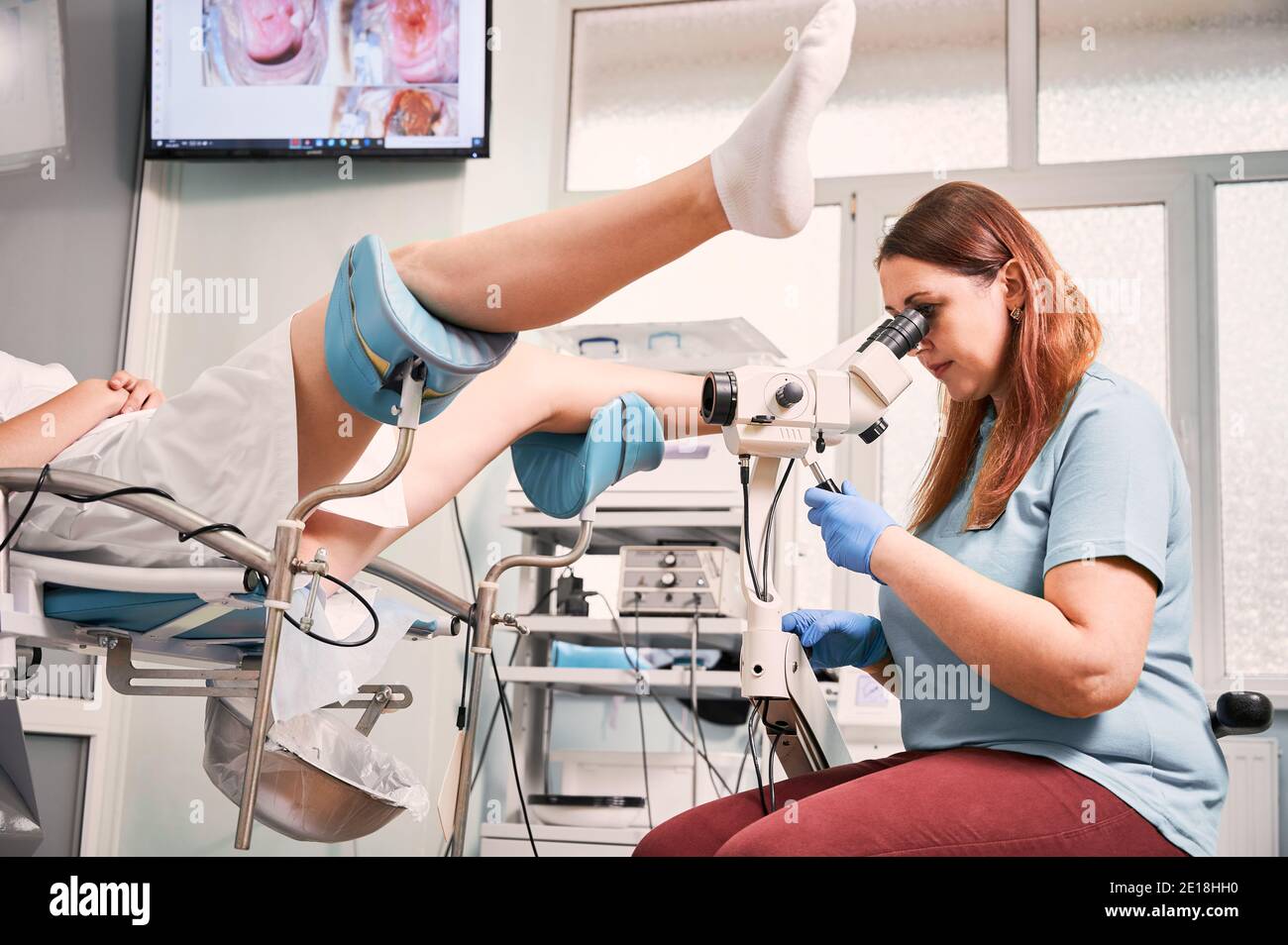
Gynäkologe mit Kolposkop während der Untersuchung Frau in der gynäkologischen Klinik. Weibliche Patientin legt in gynäkologischen Stuhl. Konzept der Gynäkologie, medizinische Untersuchung und weibliche Gesundheit Stockfotografie - Alamy
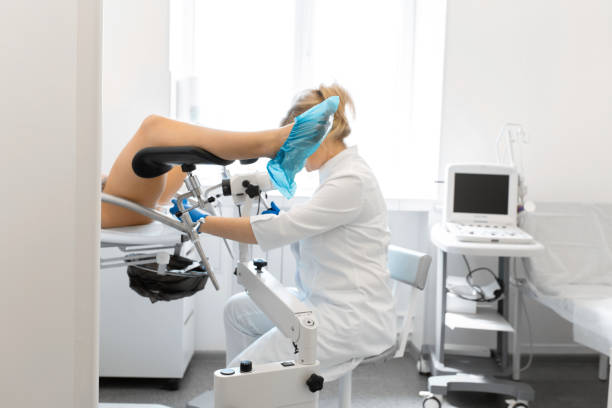
Ein Gynäkologe Untersucht Einen Patienten Auf Einem Gynäkologischen Stuhl Workflow Eines Gynäkologen Stockfoto und mehr Bilder von Gynäkologe - iStock

1.200+ Fotos, Bilder und lizenzfreie Bilder zu Frauenarzt Stuhl - iStock | Frauenarzt untersuchung, Gynäkologische untersuchung, Frauenarzt besuch
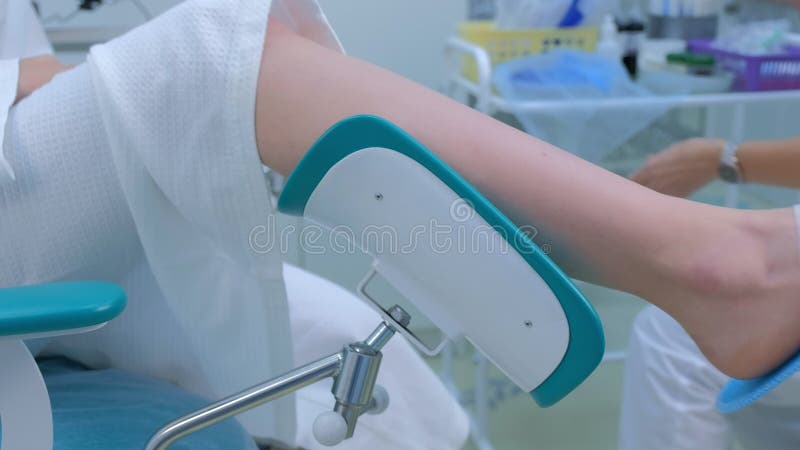
Patienten Frau in Einem Gynäkologischen Stuhl in Der Klinik Seitenansicht-Beinnahaufnahme. Stock Footage - Video von zuhause, beratung: 193002012